Topology of Numbers - IV

(Linear Fractional Transformations. Chapter 3 of Topology of Numbers.)

We want to study the symmetries of the Farey diagram. Symmetries will be invertible transformations that take vertices to vertices, edges to edges and triangles to triangles.

Symmetries of the Farey Diagram

Consider linear transformations for points in \( \mathbb{R}^2 \).

$$T \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix}a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} a x + by \\ c x + d y \end{pmatrix}$$

If we associate \( (x,y) \) to the fraction \( x/y \), then we get,

$$T \left( \frac{x}{y} \right) = \frac{ a (x/y) + b}{c (x/y) + d}$$

A linear fractional transformation is defined as \(T(z) \), where

$$T(z) = \frac{a z + b}{c z + d}$$

If \(a,b,c,d\) are integers, then in general \(T(x/y)\) will be a rational number and hence a vertex of the Farey diagram. We would also like \(T\) to preserve the edges of the Farey diagram which leads to the following proposition:

We will use \( LF(\mathbb{Z}) \) to denote the set of all linear fractional transformations. A useful fact for \(T\) in \( LF(\mathbb{Z}) \) is that its inverse is also in \( LF(\mathbb{Z}) \).

$$\begin{pmatrix}a & b \\ c & d \end{pmatrix}^{-1} = \frac{1}{ad - bc} \begin{pmatrix}d & -b \\ -c & a \end{pmatrix}$$

If \(a,b,c,d\) are integers and \( a d - bc = \pm 1\), then inverse also has integer entries and determinant \( \pm 1 \).

Since each linear fractional transformation \(T\) not only sends vertices to vertices but also edges to edges, \(T \) also preseves triangles in the Farey diagram. Moreover, since each \(T \) has an inverse, it defines a one-to-one and onto transformation of vertices, edges and triangles.

A useful proptery of linear fractional transformations is that we can know everything about a given transformation if we determine the effect on a single triangle. This is because a given triangle determines all its adjacent triangles and so on.

It turns out (we will see without proof) that there are seven ways that elements of \( LF(\mathbb{Z})\) can act on the Farey diagram. Here is the how the circular Farey diagram looks like:

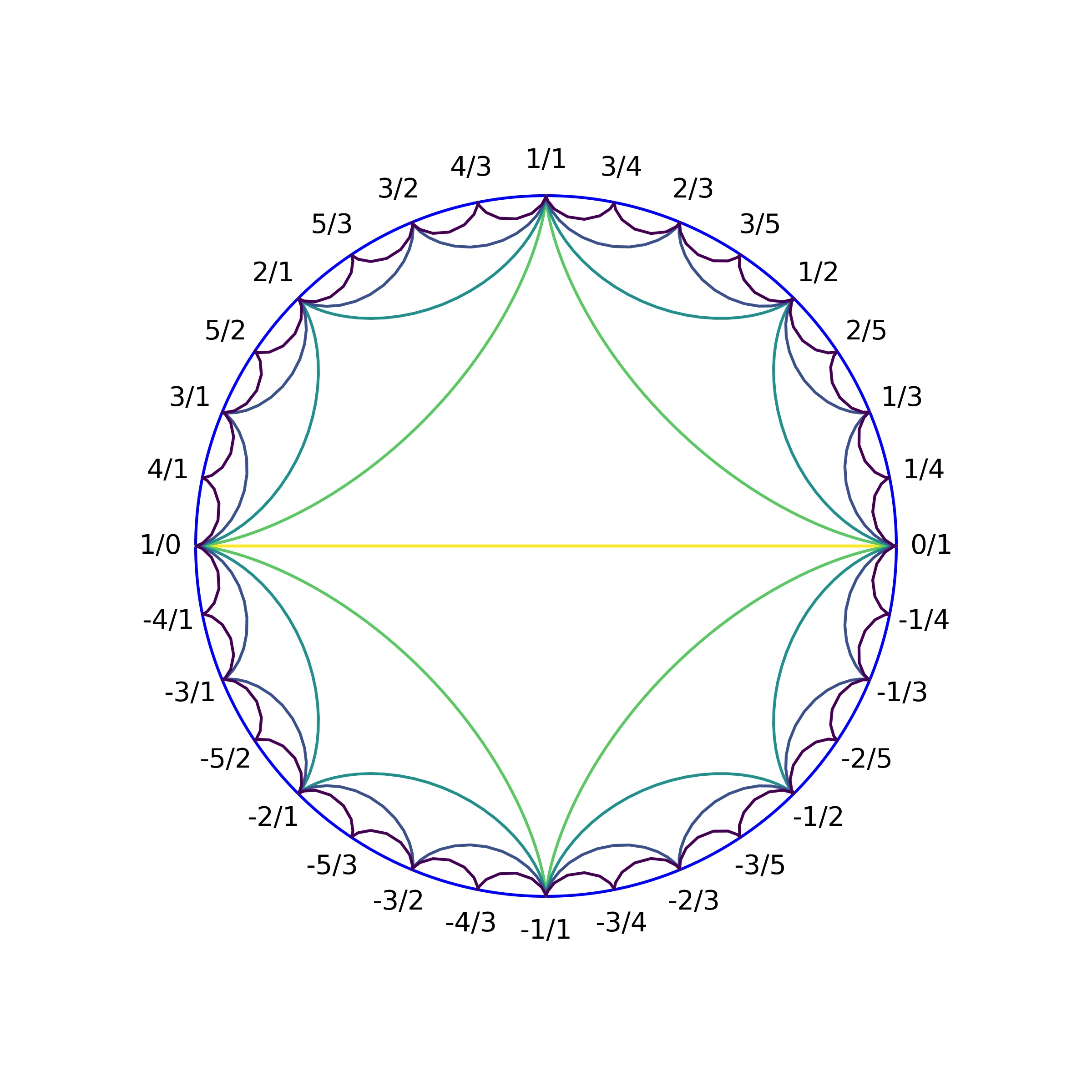
1. \(T(x/y) = y/x \) with matrix \( \begin{pmatrix}0 & 1 \\ 1 & 0 \end{pmatrix} \) gives a reflection of the Farey diagram across its vertical axis.

2. \(T(x/y) = -x/y \) with matrix \( \begin{pmatrix}-1 & 0 \\ 0 & 1 \end{pmatrix} \) gives a reflection of the Farey diagram across its horizontal axis.

3. \(T(x/y) = -y/x \) with matrix \( \begin{pmatrix}0 & 1 \\ -1 & 0 \end{pmatrix} \). This is a composition of 1 and 2 (changing the order adds an overall minus sign to the matrix, and leaves the fraction unaffected). This is an inversion in the origin.

4. \(T(x/y) = y/(y-x) \) corresponding to the matrix \( \begin{pmatrix}0 & 1 \\ -1 & 1 \end{pmatrix} \). This has the effect of rotating the triangle \(\langle 1/0,0/1,1/1 \rangle \) about its centerpoint to \( \langle 0/1, 1/1, 1/0 \rangle \). The entire Farey diagram is rotated about the same point.

5. \(T(x/y) = x/(X+y) \) corresponding to the matrix \( \begin{pmatrix}1 & 0 \\ 1 & 1 \end{pmatrix} \). Note that \(0/1 \) is a fixed point. Generally \( T(1/n) = 1/(n+1) \). Thus the triangle \( \langle 0/1,1/0,1/1 \rangle \) is taken to \( \langle 0/1,1/1,1/2 \rangle \).

6. \(T(x/y) = (2x+y)/(x+y) \) corresponding to the matrix \( \begin{pmatrix}2 & 1 \\ 1 & 1 \end{pmatrix} \). To understand this transformation, consider an infinite strip :

T leads a to translation of one unit to the right.

1. \(T(x/y) = (x+y)/x \) corresponding to the matrix \( \begin{pmatrix}1 & 1 \\ 1 & 0 \end{pmatrix} \). Consider the same strip as above, T translates each triagnle half a unit to the right and reflect it across the horizontal axis of the strip. Such a motion is called a glide reflection. Performing this motion twice yield the transformation in 6.

Hence, there are seven types of symmetries of the Farey diagram:

1. reflection across an edge
2. reflection across a line perpendicular to an edge
3. rotation about centerpoint of an edge
4. rotation about centerpoint of a triangle
5. rotation about a vertex
6. translation of periodic infinite strip
7. glide-reflection of periodic infinite strip

Specifying where a Triangle goes

We will see that there is always an element of \( LF(\mathbb{Z}) \) which any triangle to any other triangle; and we can also specify where each vertex goes.